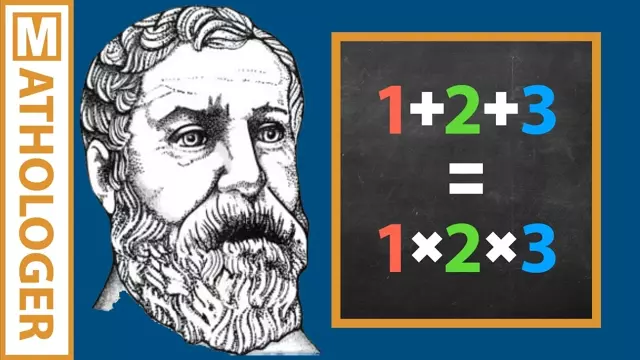Heron’s formula: What is the hidden meaning of 1 + 2 + 3 = 1 x 2 x 3 ?

2022-05-14

[public] 109K views, 14.6K likes, dislikes audio only

Today's video is about Heron's famous formula and Brahmagupta's and Bretschneider's extensions of this formula and what these formulas have to do with that curious identity 1+2+3=1x2x3.

00:00 Intro

01:01 1+2+3=1x2x3 in action

02:11 Equilateral triangle

02:30 Golden triangle

03:09 Chapter 1: Heron

06:18 Heron's formula

08:50 Brahmagupta's formula

10:20 Bretschneider's formula

11:52 Chapter 2: How? The proof

12:57 Heron via trig

20:09 Cut-the-knot

21:16 Albrecht Hess

21:46 Heron to Brahmagupta proof animation

25:10 Thank you!

Heron's formula on the Cut-the-knot site:

https://www.cut-the-knot.org/Curriculum/Geometry/HeronsFormula.shtml

Original article by Roger B. Nelsen "Heron's formula via proofs without words", featuring a version of the nice rectangle proof that I am presenting in this video: https://www.maa.org/sites/default/files/0746834212944.di020798.02p0691h.pdf

Simple derivation of Heron's formula just using Pythagoras's theorem:

https/www.mathpages.com/home/kmath196/kmath196

Job Bouwman's maths posts on Quora (you'll have to scroll a bit to get to Heron's formula)

http://shorturl.at/gzGOX

http://shorturl.at/dBX12

https://www.quora.com/profile/Job-Bouwman

A very comprehensive book about quadrilaterals:

Claudia Alsina, Roger B. Nelsen - A Cornucopia of Quadrilaterals (Dolciani Mathematical Expositions) (2020, American Mathematical Society)

Albrecht Hess's paper "A Highway from Heron to Brahmagupta"

https://forumgeom.fau.edu/FG2012volume12/FG201215.pdf

If you liked the rectangle proof of the sum = product identity you'll probably also like this proof of Pythagoras's theorem:

https://youtu.be/r4gOlttnJ_E

I also mentioned this one earlier in a video on this main channel

https://youtu.be/r4gOlttnJ_E

Two more interesting notes on the cut-the-knot page:

1. Let the angles of the triangle be 2α, 2β, 2γ so that α + β + γ = 90°. The identity RGP = r²(R + G + P) is equivalent to the following trigonometric formula: cotα + cotβ + cotγ = cotα cotβ cotγ, where "cot" denotes the standard cotangent function. More on this here https://tinyurl.com/yrsuhthk

2. A supercute way to derive Pythagoras from Heron with one line of calculus

https://www.cut-the-knot.org/pythagoras/HeronsDerivative.shtml

For a cyclic quadrilateral that also has an incircle we have a+b=c+d and it follows that the area is just square root of the product of all of the sides.

A 3d counterpart to Heron's formula:

https://en.wikipedia.org/wiki/Heron%27s_formula#Heron-type_formula_for_the_volume_of_a_tetrahedron

A different 3d connection (de Gua's theorem)

https://www.mathpages.com/home/kmath226/kmath226.htm

A couple of links to get you started on generalisations involving cyclic n-gons:

https://arxiv.org/pdf/1203.3438.pdf

https://arxiv.org/pdf/1910.08396.pdf

https://tinyurl.com/tyhzwpxj

Another interesting observation extending the fact that the 3-4-5 right-angled triangle has incircle radius 1: In general, the incircle radius of any right-angled triangle with integer sides is an integer.

Have a look at this for a related proof that arctan 1 + arctan 2 + arctan 3 = pi:

https://www.geogebra.org/m/A65eMkuN

https://math.stackexchange.com/questions/197393/why-does-tan-11-tan-12-tan-13-pi (2nd proof)

Not many integer solutions for x+y+z=xyz:

0+0+0=0x0x0

1+2+3=1x2x3

(-1)+(-2)+(-3)=(-1)x(-2)x(-3)

Other interesting little curiosities (some mentioned in the comments):

2+2=2x2=2^2 (of course)

3^3+4^3+5^3=6^3 = 6*6*6=216 illuminati confirmed

6+9+6*9 = 69

a+9+a*9 = 10a+9 (sub any digit)

https://en.wikipedia.org/wiki/Mathematical_coincidence

log(1+2+3)=log(1)+log(2)+log(3) follow from 1+2+3=1x2x3

Grégoire Locqueville 2:32 "Maybe one of you can check in the comments" is the new "left as an exercise to the reader" :)

Scaling the equations at this time code: /youtube/video/IguNXoCjBEk

length, area and "volume" start out the same with radius 1: length=area=volume.

When you scale by r, these values scale in this way Length = length * r, Area = area * r^2 and Volume = "volume" r^3. Therefore, Length = length * r = area *r and so (multiply through with r) Length* r = area *r ^2 = Area, etc.

Typo spotted: At the very end, in Brahmagupta's Formula the third bracket should be (A+C+D-B) not (A+B+D-B).

X minus Y maths t-shirt: Sadly the etsy shop I got this one from seems to have disappeared (Pacific trader). There is what appears to be a ripoff on zazzle by someone who does not know what they are doing :) https://tinyurl.com/24vrzpu9

Nice variation of the t-shirt joke by one of you: M - I - I = V :)

The Chrome extension I mentioned in this video is called CheerpJ Applet runner.

Music used in this video: Aftershocks by Ardie Son and Zoom out by Muted

Enjoy!

Burkard