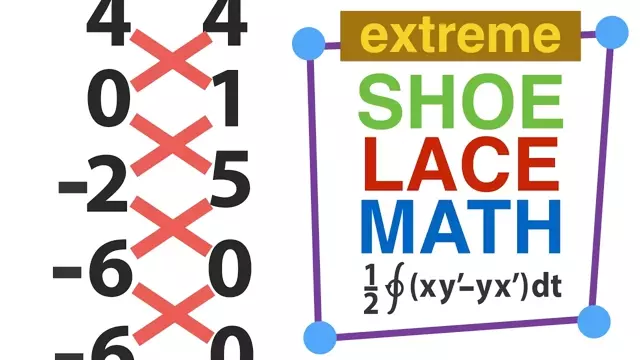2017-06-10

[public] 158K views, 6.31K likes, 54.0 dislikes audio only

Mathologer

Gauss's shoelace formula is a very ingenious and easy-to-use method for calculating the area of complicated shapes. In this video I tell you how to use this formula and I let you in on the mathematical area-cancelling magic that powers it. Other highlights include a very cute animated proof of the area interpretation of 2x2 determinants, a really elementary high-school level proof of the integral area formula for parametric curves that's usually only derived in university level multivariable calculus. Oh, and you'll also see the integral formula in action when I calculate the surprisingly nice value of the deltoid rolling curve that played an important role in the Kakeya needle problem video.

As usual thank you very much to Marty Ross and Danil Dimitriev for their help with this video.

Enjoy!