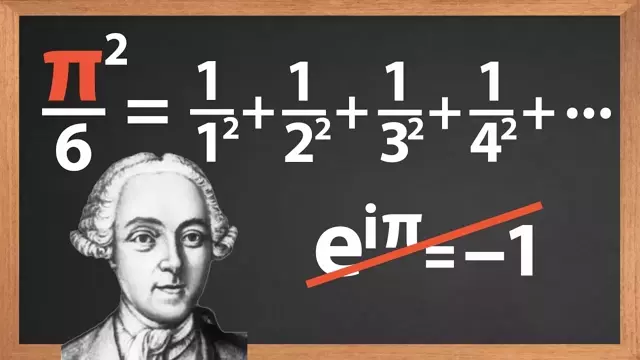2017-08-11

[public] 753K views, 23.1K likes, 371 dislikes audio only

Mathologer

NEW (Christmas 2019). Two ways to support Mathologer

Mathologer Patreon: https://www.patreon.com/mathologer

Mathologer PayPal: paypal.me/mathologer

(see the Patreon page for details)

I've got some good news and some bad news for you. The bad news is that Euler's identity e to the i pi = -1 is not really Euler's identity. The good news is that Euler really did discover zillions of fantastic identities. This video is about the one that made him famous pretty much overnight: pi squared over 6 = the infinite sum of the reciprocals of the square natural numbers. This video is about Euler's ingenious original argument which apart from this superfamous identity allowed him to evaluate the precise values of the zeta function at all even numbers (amongst many other things :)

I am a huge fan of Euler’s and had been wanting to to make this video for a long time. Pretty nice how it did come together I think. One of the things I like best about making these videos is how much I end up learning myself. In this particular instance the highlights were actually calculating those other sums I mention myself using Euler’s idea (the Riemann Zeta function evaluated at even numbers) as well as learning about this alternate way to derive the Leibniz formula using the zeros of 1-sin(x). Oh, and one more thing. Euler’s idea of writing sin(x) in terms of its zeros may seem a bit crazy, but there is actually a theorem that tells us exactly what is possible in this respect. It’s called the Weierstrass factorization theorem.

Good references are the following works by Euler: http://www.17centurymaths.com/contents/introductiontoanalysisvol1.htm

http://eulerarchive.maa.org//docs/translations/E352.pdf

The t-shirt I am wearing in this video is from here: https://shirt.woot.com/offers/pi-rate?ref=cnt_ctlg_dgn_1

Thank you very much for Marty Ross and Danil Dmitriev for their feedback on an earlier draft of this video and Michael Franklin for his help with recording this video..

Enjoy!

Typo around 16:30: In the product formula for 1-sin x every second factor should feature a (1+...) instead of a (1-...). So the whole thing starts like this: (1 - 2 x/Pi)^2 (1 + 2 x/(3 Pi))^2 (1 - 2 x/(5 Pi))^2 (1 + 2 x/(9 Pi))^2... :)