The Game You Can't Win

2020-05-12

[public] 1.30M views, 75.6K likes, 1.58K dislikes audio only

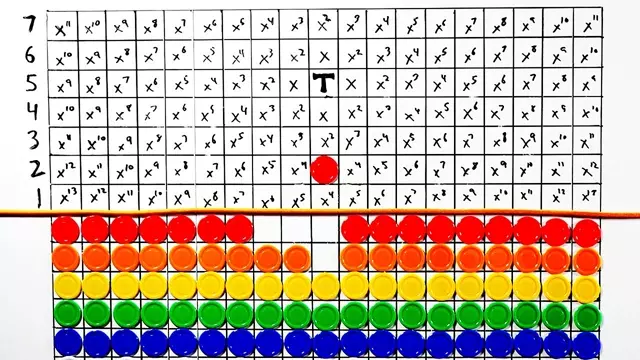
4K

John Conway’s work stretched from nearly-inaccessible math theory to fun children’s games, and it defined how we thought about recreational mathematics in the 20th century. Conway’s Soldiers is the perfect example of a Conway-esque math game: the rules are simple, the gameplay is easy, and it becomes very hard very quickly… and in this case of a basic checkers game, it packs a surprising punch of becoming literally impossible for a reason that isn’t even close to obvious.

But the mathematical importance doesn’t end with an unexpected reveal of impossibility. Conway found that the secret to *why* it’s impossible depends on the Golden Ratio of 1.618, which has fascinated mathematicians since Pythagoras and Euclid. We see the Golden Ratio in aesthetically-pleasing magazine layouts, flower patterns, and pretty faces, but John Conway showed us that it’s at the heart of why we can’t reach the fifth row of a checker game.

Play the game yourself with the online simulator and check out Zvezdelina Stankova’s proof on Numberphile. It’ll make sense. John Conway may be gone now, but we’ll be playing his games and poring over his ideas for centuries.

Conway Checkers (proof), Numberphile2 | Zvezdelina Stankova: /youtube/video/Or0uWM9bT5w

Conway’s Soldiers Interactive Game (Clever Learning): https://www.cleverlearning.co.uk/blogs/blogConwayInteractive.php

*** SOURCES ***

Berlekamp, E. R.; Conway, J. H; and Guy, R. K. "The Solitaire Army." In Winning Ways for Your Mathematical Plays, Vol. 2: Games in Particular. London: Academic Press, pp. 715-717 and 729, 1982.

Honsberger, Ross. "A Problem in Checker Jumping." Ch. 3 in Mathematical Gems II. Washington, DC: Math. Assoc. Amer., pp. 23-28, 1976.

Tatham, Simon and Taylor, Gareth. “Reaching Row Five in Solitaire Army.” https://tartarus.org/gareth/maths/stuff/solarmy.pdf

plus magazine, “Mathematical Mysteries: The Solitaire Advance.” https://plus.maths.org/content/os/issue12/xfile/index

Bell, George. “The Peg Solitaire Army.” http://www.gibell.net/pegsolitaire/army/index.html

Bell, Hirschberg, Guerrero-Garcia. “The Minimum Size Required of a Solitaire Army.” https://arxiv.org/pdf/math/0612612.pdf

Taylor, Jasper. “Conway’s Soldiers.” https://sites.math.washington.edu/~morrow/336_10/papers/jasper.pdf

John Conway’s obituary, New York Times: https://www.nytimes.com/2020/04/15/technology/john-horton-conway-dead-coronavirus.html

Roberts, Siobhan. “Genius at Play: The Curious Mind of John Horton Conway” (2015). https://www.amazon.com/Genius-At-Play-Curious-Horton-ebook/dp/B00UX2UR44

*** LINKS ***

Vsauce2:

Twitter: https://twitter.com/VsauceTwo

Facebook: https://www.facebook.com/VsauceTwo

Talk Vsauce2 in The Create Unknown Discord: https://discord.gg/tyh7AVm

Hosted and Produced by Kevin Lieber

Instagram: http://instagram.com/kevlieber

Twitter: https://twitter.com/kevinlieber

Podcast: https://www.youtube.com/thecreateunknown

Research and Writing by Matthew Tabor

https://twitter.com/TaborTCU

Editing by John Swan

https://www.youtube.com/channel/UCJuSltoYKrAUKnbYO5EMZ2A

Huge Thanks To Paula Lieber

https://www.etsy.com/shop/Craftality

"Binary Max Escape" by Basswaite: https://distrokid.com/hyperfollow/basswaite/binary-max-escape-2

Select Music By Jake Chudnow: http://www.youtube.com/user/JakeChudnow

Get Vsauce's favorite science and math toys delivered to your door!

https://www.curiositybox.com/

#education #vsauce2 #maths